esssup - inf sup math : 2024-10-31 esssupIn mathematics, the concepts of essential infimum and essential supremum are related to the notions of infimum and supremum, but adapted to measure theory and functional analysis, where one often deals with statements that are not valid for all elements in a set, but rather almost everywhere, that is, except . See more esssupThe LV Capacitor is a block added by Immersive Engineering. The LV Capacitor stores 100,000 RF inside it, and has an input and output of 256 RF maximum. RF stored in the LV Capacitor is kept if the block is broken. To read the current value inside of the LV Capacitor use the Engineer's Voltmeter.
Consideration of LV volume, mass, and relative wall thickness (or mass/volume) allows classification of LV remodeling that includes virtually all LV remodeling changes that are seen in health and disease.
esssup
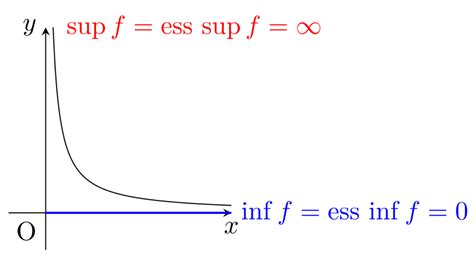
The essential supremum is the proper generalization to measurable functions of the maximum. The technical difference is that the values of a function on a set of measure zero don't affect the essential . Does the essential supremum $esssup(f_{\omega})_{\omega \in \Omega}$ of a collection of measureable functions exist? 0 show that $\|f\|_{\infty} = \sup_{x \in .Learn the definition and properties of the essential supremum and infimum of a family of real-valued random variables on a probability space. See examples, proofs and . 本质上确界 (ess sup) 是一种在测度大于0的自变量集合上的最大值,与常规的最大值 (sup) 有所区别。本文用图示和解释说明了本质上确界的定义和性质,并给出了相关的例子和应用。
esssup Essential supremum is a generalization of the maximum of a function that only exceeds a number on a set of measure zero. Learn how to define and use .inf sup mathesssup X jfj<1: De nition 7.4. Let (X;A; ) be a measure space. The space L1(X) consists of pointwise a.e.-equivalence classes of essentially bounded measurable functions f: X!R .
The Fondation App. Download the new Fondation Louis Vuitton app, free access. It offers exclusive sections to prepare, to approach, to visit and to extend your experience. Discover new content about the current exhibitions through interviews with the curators.
esssup